题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1

1 2 2

2 3 2

2 4 1

1 3 5

3 4 3

1 4 4

输出样例#1：

0 2 4 3

说明

时空限制： 1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

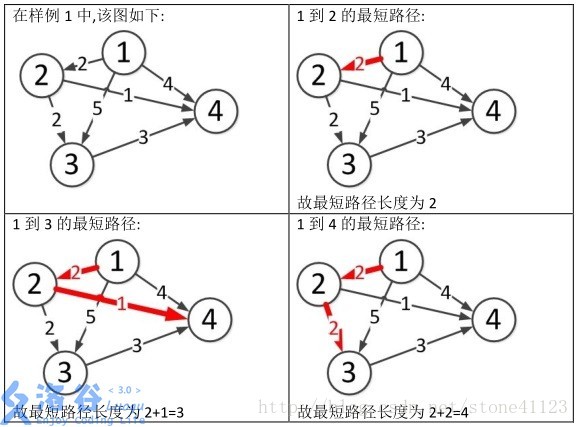
样例说明：

我第一次用的裸的SPFA，结果被cin坑了，1800多ms

然后改了scanf，660ms。。。。

嗯，贴代码吧：

#include
     
      #define inf 2147483647using namespace std;struct edge{    int to,next,w;};int n,m,s;edge e[500001];int head[10001];int d[10001];int f[10001];queue
      
        q;int main(){    scanf("%d %d %d",&n,&m,&s);    for(int i=1;i<=m;i++){        int x,y,nm;        scanf("%d %d %d",&x,&y,&nm);        e[i].next=head[x];        e[i].to=y;        e[i].w=nm;        head[x]=i;    }    for(int i=1;i<=n;i++){        d[i]=inf;    }    d[s]=0;    f[s]=1;    q.push(s);    while(!q.empty()){        int k=q.front();        q.pop();        f[k]=0;        for(int i=head[k];i!=0;i=e[i].next){            if(d[k]+e[i].w